Nhận dạng các hình hình học: đoạn thẳng, đường thẳng, hình tam giác, tứ giác, hình chữ nhật, hình vuông, hình thang, hình bình hành, hình thoi, hình tròn.
Dưới đây là lý thuyết (cách nhận biết) các hình hình học và sau đó là ví dụ bài tập có lời giải.
1. Đoạn thẳng
Nối 2 điểm A và B, ta thu được đoạn thẳng AB. Các điểm A và B được gọi là hai đầu mút của đoạn thẳng.
![]()
2. Đường thẳng
Kéo dài mãi đoạn thẳng AB về hai phía, ta được đường thẳng AB.

3. Tam giác
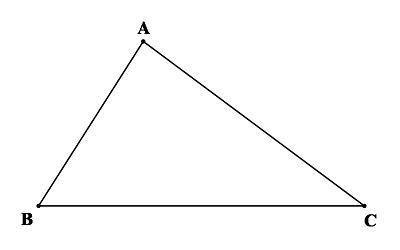
Hình tam giác có 3 đỉnh, 3 cạnh và 3 góc.
– Tam giác ABC có 3 đỉnh là A, B, C; có 3 cạnh là AB, BC và AC; có 3 góc là góc A, góc B và góc C.
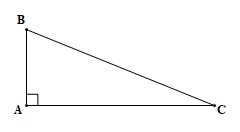
Tam giác ABC có một góc vuông gọi là tam giác vuông.
4. Tứ giác
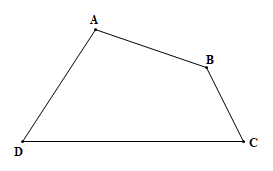
Hình tứ giác có 4 đỉnh, 4 cạnh và 4 góc.
Tứ giác ABCD có 4 đỉnh là A, B, C, D; có 4 cạnh là AB, BC, CD, AD; có 4 góc là góc A, góc B, góc C và góc D
5. Hình chữ nhật
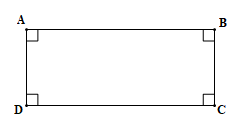
Hình chữ nhật là một tứ giác có bốn góc vuông
Hình chữ nhật ABCD có hai chiều dài AD và BC bằng nhau và song song với nhau; hai chiều rộng AB và CD bằng nhau và song song với nhau.
6. Hình vuông
Hình vuông là tứ giác có 4 cạnh bằng nhau và 4 góc vuông
– Hình vuông là hình chữ nhật có 4 cạnh bằng nhau
Hình vuông ABCD có 4 cạnh AB, BC, CD và AD đều bằng nhau.
7. Hình thang
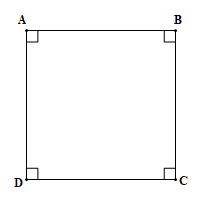
Hình thang là tứ giác có hai cạnh song song.
– Hình thang ABCD có hai cạnh AD và BC song song, AD là đáy nhỏ, BC là đáy lớn, AB và DC là các cạnh bên.
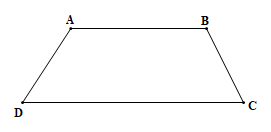
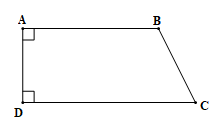
– Hình thang ABCD có các góc A, góc B vuông là hình thang vuông.
8. Hình bình hành
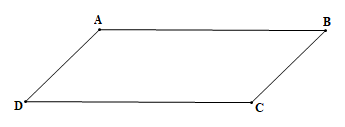
Hình bình hành là tứ giác có 2 cặp cạnh đối song song và bằng nhau.
– Hình bình hành ABCD có hai cạnh AB và CD song song với nhau và bằng nhau, hai cạnh AD và BC song song và bằng nhau.
9. Hình thoi
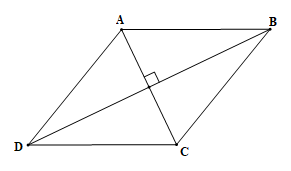
Hình thoi ABCD có: AB = BC = CD = AD, hai đường chéo AC và BD vuông góc với nhau.
10. Hình tròn
Điểm O là tâm của hình tròn. Đường bao quanh hình tròn gọi là đường tròn.
Đoạn thẳng nối tâm O với một điểm nằm trên đường tròn gọi là bán kính.
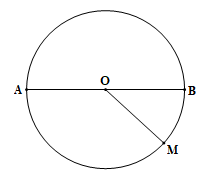
Các bán kính của đường tròn đều bằng nhau, các đoạn OA, OB, OM là các bán kính.
Đoạn thẳng nối 2 điểm trên đường tròn và đi qua tâm gọi là đường kính, đoạn AB gọi là đường kính.
Các ví dụ kèm hướng dẫn giải:
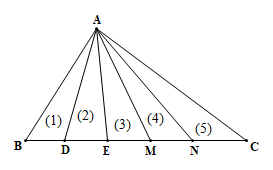
Ví dụ 1. Cho tam giác ABC, trên cạnh BC ta lấy 4 điểm D, E, M, N. Nối đỉnh A với 4 điểm vừa lấy. Hỏi đếm được bao nhiêu tam giác trên hình vẽ?
Cách 1. (Phương pháp liệt kê)
Có 5 tam giác chung cạnh
AB là ABD, ABE, ABM, ABN, ABC.
Có 4 tam giác chung cạnh AD là: ADE, ADM, AND, ADC.
Có 3 tam giác chung cạnh AE là: AEM, AEN, AEC.
Có 2 tam giác chung cạnh AM là: AMN, AMC.
Có 1 tam giác chung cạnh AN là: ANC.
(Các tam giác đếm rồi ta không đếm lại nữa).
Vậy số tam giác ta đếm được trên hình vẽ là:
5 + 4 + 3 + 2 + 1 = 15 (tam giác).
Cách 2.
(Phương pháp lắp ghép) Nhìn trên hình vẽ ta thấy:

Có 5 tam giác đơn: (1), (2), (3), (4), (5).
Có 4 tam giác ghép đôi: (1) + (2), (2) + (3), (3) + (4), (4) + (5).
Có 3 tam giác ghép 3 là: (1) +(2) +(3), (2) +(3) +(4), (3) +(4) +(5).
– Có 2 tam giác ghép 4 là: (1) + (2) + (3) +(4), (2) + (3) + (4) + (5).
– Có 1 tam gíac ghép 5 là: (1) + (2) + (3) + (4) + (5).
Vậy số tam giác đếm được là:
5 + 4 + 3 + 2 + 1 = 15 (tam giác)
Cách 3:
Ta nhận xét:
Nối 2 đầu mút của mỗi đoạn thẳng tạo thành trên cạnh đáy BC với đỉnh A ta được một tam giác. Vậy số tam giác đếm được trên hình vẽ bằng số đoạn thẳng trên cạnh đáy BC. Trên cạnh đáy BC có tất cả 6 điểm B, C, D, E, M và N.
Áp dụng kết quả trong ví dụ 1 (phương pháp quy nạp) ta có số đọan thẳng đếm được là:
6 x (6 – 1) : 2 = 15 (đoạn thẳng).
Vậy ta đếm được 15 tam giác trên hình vẽ.
Cách 4. (Phương pháp quy nạp)
Ta nhận xét:
*Nếu trên cạnh BC, lấy 1 điểm và nối với điểm A thì ta đếm được:
Có 2 tam giác đơn là: (1), (2).
Có 1 tam giác ghép đôi là: (1) + (2). Tổng số tam giác đếm được là:
2 + 1 = 3 (tam giác)
*Nếu trên BC, ta lấy 2 điểm và nối với đỉnh A thì ta đếm được
Có 3 tam giác đơn là: (1), (2), (3).
Có 2 tam giác ghép đôi là: (1) +(2), (2) +(3).
Có 1 tam giác ghép 3 là: (1) + (2) + (3).
Tổng số tam giác đếm được là:
3 + 2 + 1 = 6 (tam giác)
Vậy quy luật ở đây là: Nếu trên cạnh đáy BC ta lấy n điểm và nối chúng với đỉnh A thì ta sẽ đếm được (n + 1) tam giác đơn và số tam giác đếm được là:
1 + 2 + 3 +…+ (n + 1) = (n + 2) x (n +1) : 2 (tam giác)
Áp dụng:
Trên cạnh đáy BC lấy 4 điểm thì số tam giác đơn đếm được là 5 và số tam giác đếm được là:
(4 + 2) x (4 + 1) : 2 = 15 (tam giác)
Ví dụ 2. Cần ít nhất bao nhiêu điểm để khi nối chúng lại ta được 6 đoạn thẳng?
Hướng dẫn
Ta nhận xét:
Nếu có 3 điểm thì khi nối chúng lại ta được 3 đoạn thẳng.
Nếu có 4 điểm thì khi nối chúng lại ta được:
4 x (4 – 1) : 2 = 6 (đoạn thẳng)
Vậy để nối lại được 6 đoạn thẳng ta cần ít nhất 4 điểm.
BÀI TẬP:
Bài 1. Cho 6 điểm phân biệt. Hỏi khi nối chúng lại với nhau ta được bao nhiêu đoạn thẳng? (Đs: 15 đoạn thẳng).
Bài 2. Cần ít nhất bao nhiêu điểm để khi nối chúng lại ta được 10 đoạn thẳng? (Đs: 5 điểm).
Bài 3. Cho hình thang ABCD. Trên đáy AD, ta lấy 5 điểm rồi nối đỉnh C với mỗi điểm vừa chọn. Trên đáy nhỏ BC, ta lấy 4 điểm rồi nối đỉnh A với mỗi
điểm vừa chọn. Nối AC. Hỏi có bao nhiêu tam giác được tạo thành trên hình vẽ? (Đs: 36 tam giác).
Bài 4. Cho 4 điểm trên mặt phẳng, trong đó không có 3 điển nào cùng nằm trên 1 đoạn thẳng, Hỏi khi nối lại ta thu được bao nhiêu tam giác? (Đs: 4 tam giác).
Bài 5. Cho tứ giác ABCD. Chia mỗi cạnh thành 4 phần bằng nhau rồi nối các điểm chia như hình vẽ. Hỏi đếm được bao nhiêu tứ giác? (Đs: 10 tứ giác)
Bài 6. cho hình chữ nhật ABCD có chiều dài bằng 4 cm, chiều rộng bằng 3 cm. Ta chia chiều dài thành 4 phần bằng nhau và chiều rộng thành 3 phần bằng nhau rồi nối các điểm chia như hình vẽ.
a) Có bao nhiêu hình vuông trên hình vẽ.
b) Tính tổng các chu vi và tổng các diện tích của các hình vuông tạo thành.
Đs: a) 20 hình vuông
b) 120cm và 54cm2

